Understanding Dijkstra's Algorithm
The algorithm which helps power Google Maps !
Have you ever wondered how apps like Google Maps are able to find the shortest and quickest path for you ? Or how greedy (pun intended) oil corporations lay down their gas pipelines in such a manner that the cost borne by them is the least. Or even how data is sent across the internet so quickly and effectively ?
Dijkstra's Algorithm.
Dijkstra's algorithm is an algorithm for finding the shortest paths between nodes in a graph, which may represent, for example, road networks. It was conceived by computer scientist Edsger W. Dijkstra in 1956 and published three years later.
There are many variants of the algorithm, but the one we'll be looking at today is the one in which we fix a single node as the 'source/beginning' node, and find out the shortest distance of all the other nodes in the graph from that node.

Dijkstra's algorithm is a greedy algorithm. That means that at each step of solving the problem, we make the choice that seems best at that given moment, even though it may not be the best choice in the long run.
For example, suppose you're at a crossroad, and you have 2 options. You know that taking the first road will give you a $100 and the second road will give you $50. There's a chance of getting more money down the road, but you don't know what lies ahead. Once you choose one of the roads, you can't go back.
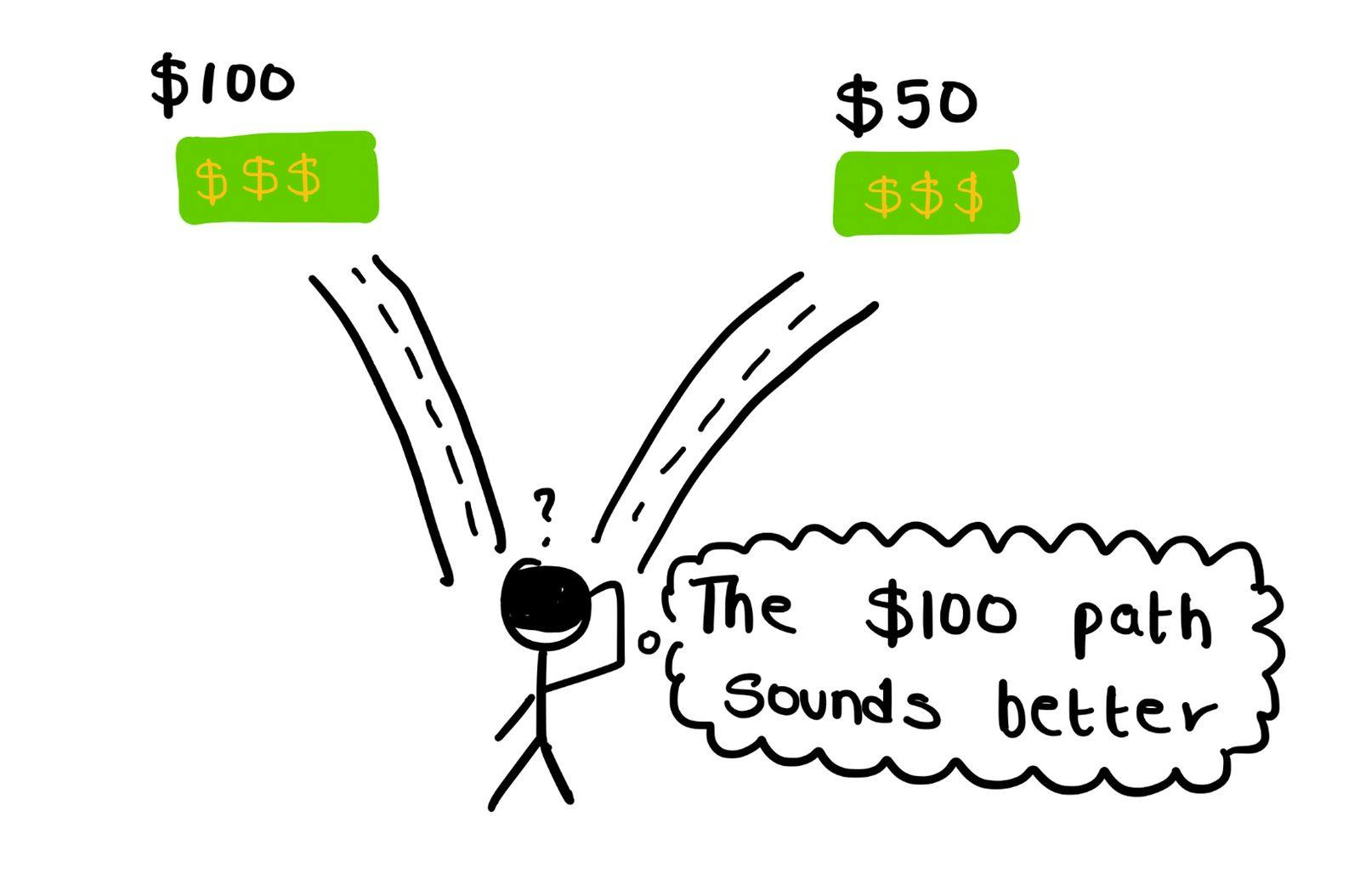
Obviously, you'd take the $100 route, since at this stage it's the path which gives you the most profit. But suppose after reaching the $100, you find out that the path ahead only gives you $2. And that if you'd taken the $50 path instead, there would been a nice fat wad of $1000 in cash waiting for you ahead. Ouch.
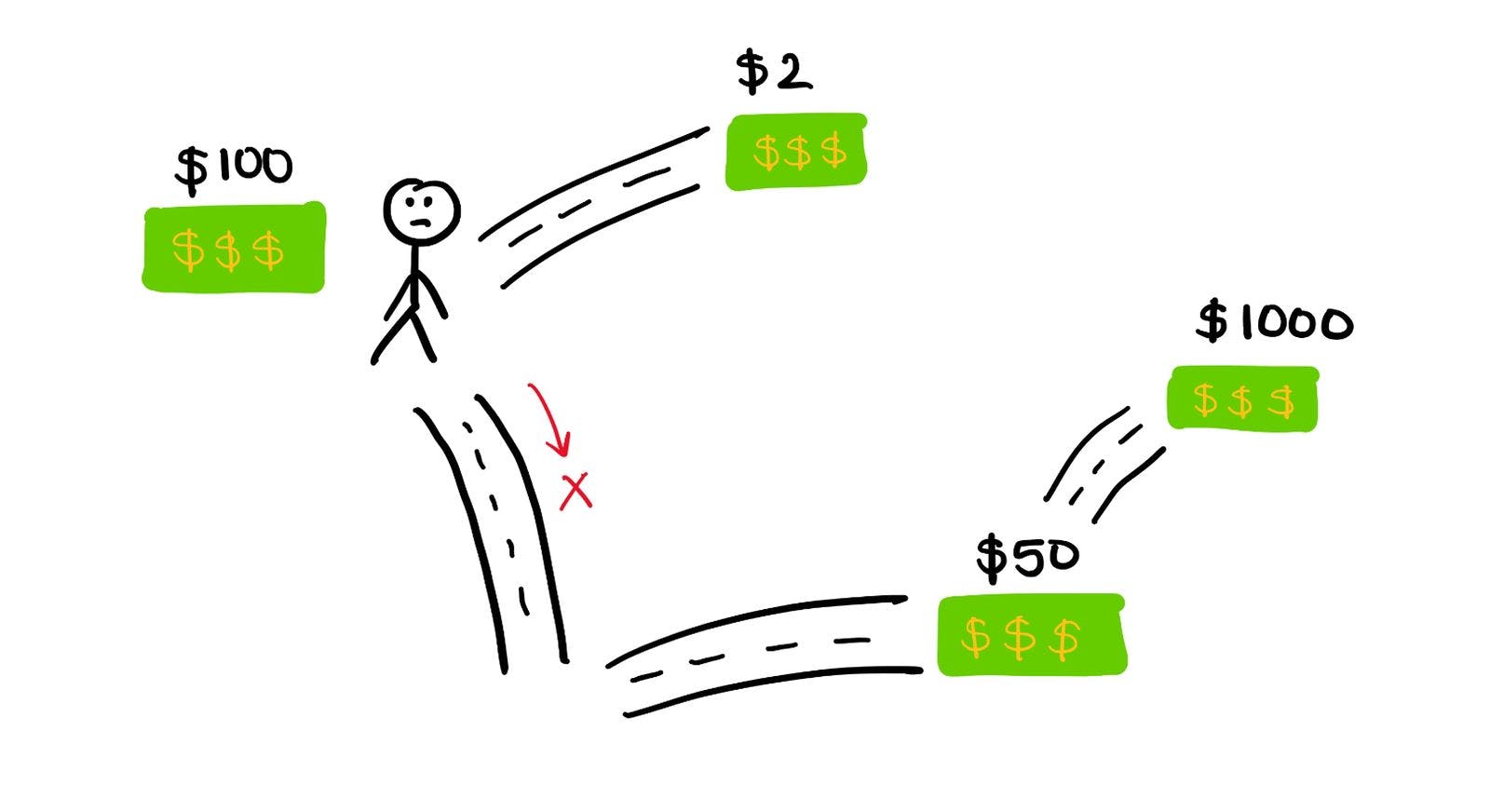
Greedy algorithms don't always necessarily give the most optimal/best result. Thankfully, Dijkstra's algorithm always gives us the optimal result (a helpful proof can be found here).
Keep in mind that the algorithm only works if the weight of the edges (the cost from going from one node in the graph to another) is positive. It will NOT work for graphs which have negative-weight edges.
Now that we've had a quick overview, let's dive into the details !
The Working
Consider the graph given below.
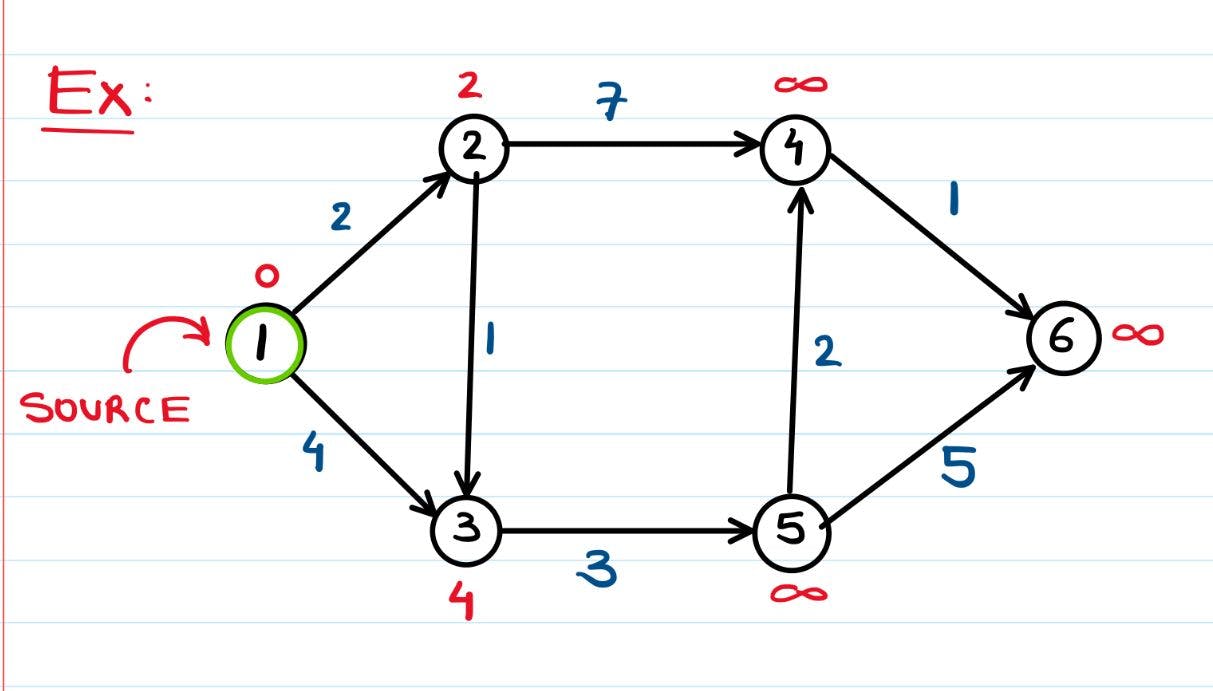
The green node labelled 1, is our source/starting node. Our goal is to find the shortest distance between our starting node, and all the other nodes in the graph. For example, the path from 1->4 could be:
- 1->3-5->4, with a total distance/cost of 4+3+2=9 or
- 1->2->4, with a total distance of 2+7=9
- Or any other valid path.
Note that a directed arrow from 1->2 means we can travel from node 1 to node 2, but not the other way around.
While it may seem easy to calculate these shortest distances by looking at this graph, it gets far harder when the number of nodes increases. We'll understand how the algorithm works by looking at this small example.
The blue numbers above each edge represent the distance between the connected nodes. For example, the distance from node 3 to node 5 is 3 units. The red numbers above each node, indicate the distance of that node from the starting node (node 1). We assume that we initially know the distances of the nodes directly connected to node 1 (node 2 and 3), and that the rest of the nodes are at an infinite distance, since at this point we have no idea how far they really are.
The way we're going to find the shortest distance of a node from node 1, is by using relaxation.
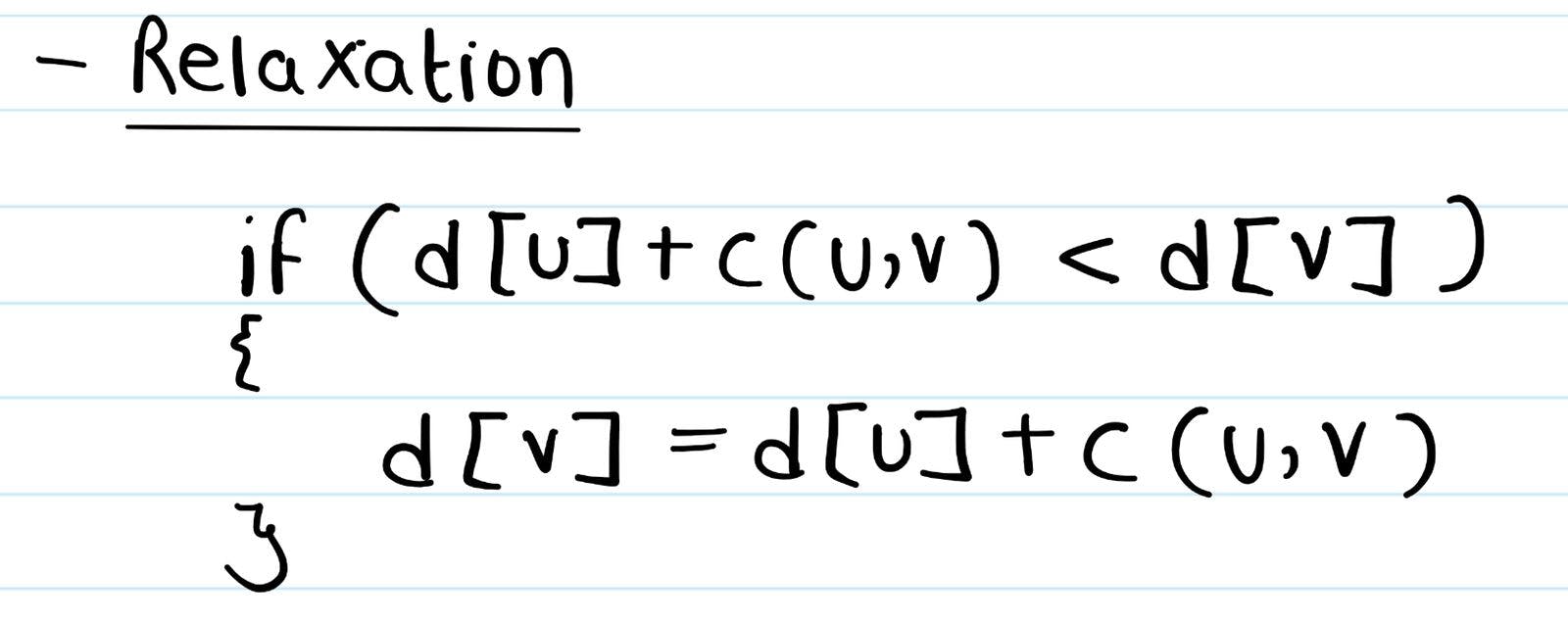
This definitely seems confusing, but let's break it down.
- 'u' is the node we're currently at
- 'v' is a node which is connected to 'u' (u->v exists)
- d[u] is the distance from node 1 to node u
- c(u, v) is the direct distance between u and v (or the blue number on top of the edge)
- d[v] is the distance from node 1 to node v
So what we're basically saying is that if we're at a node 'u', we can help find the shortest distance from node 1 to the nodes connected to 'u', by using the above formula. Node 'u' tells it's neighbors that, "Hey, I know that your distance from 1 is d[v]. But if you take the path through me, you can reduce that distance".
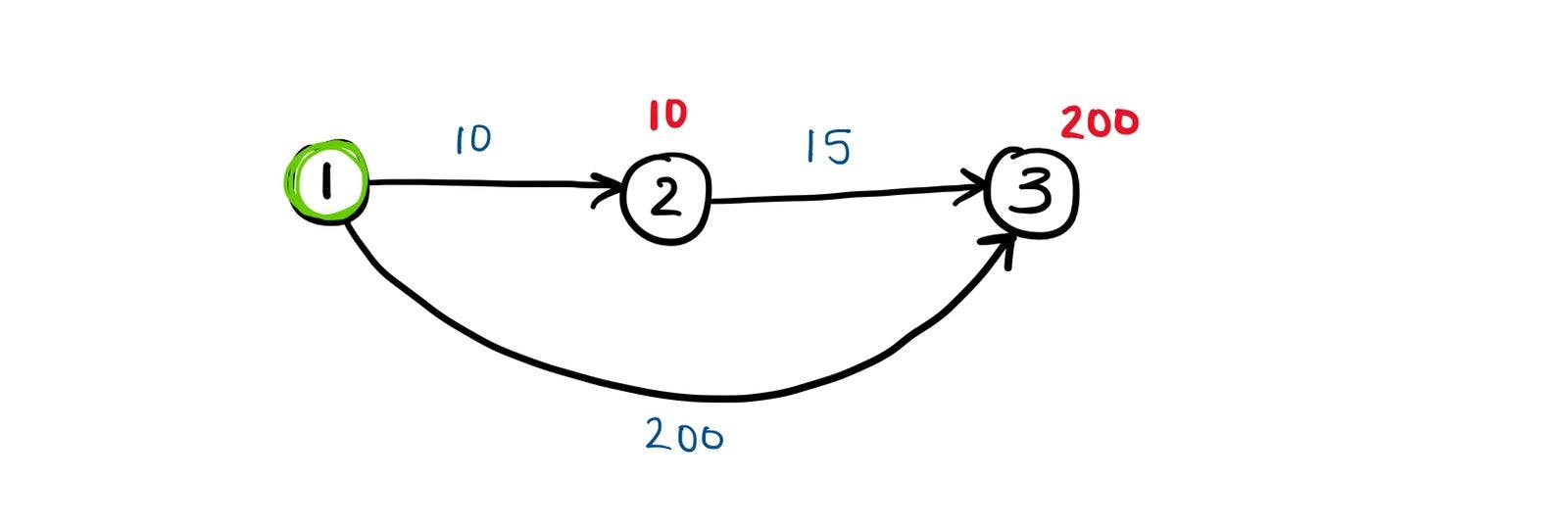
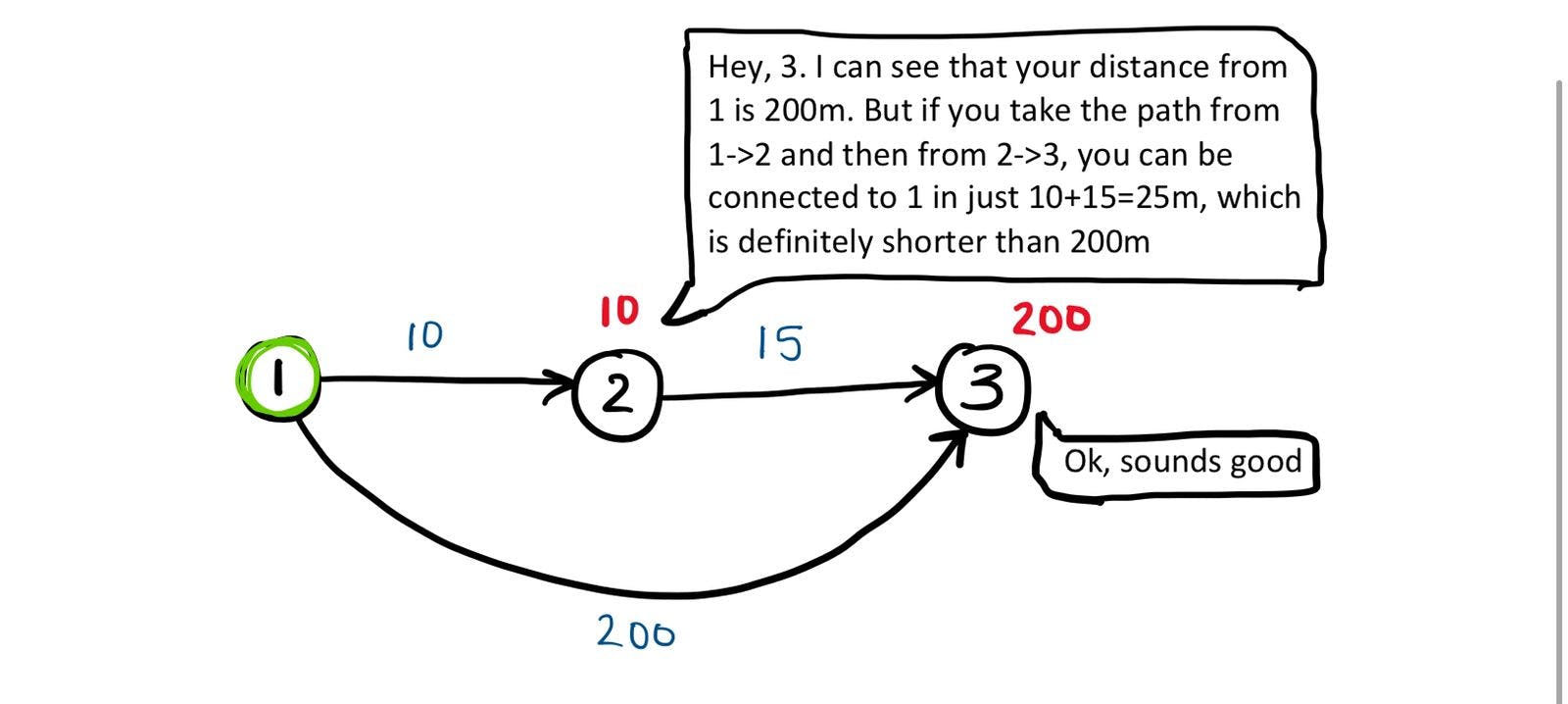
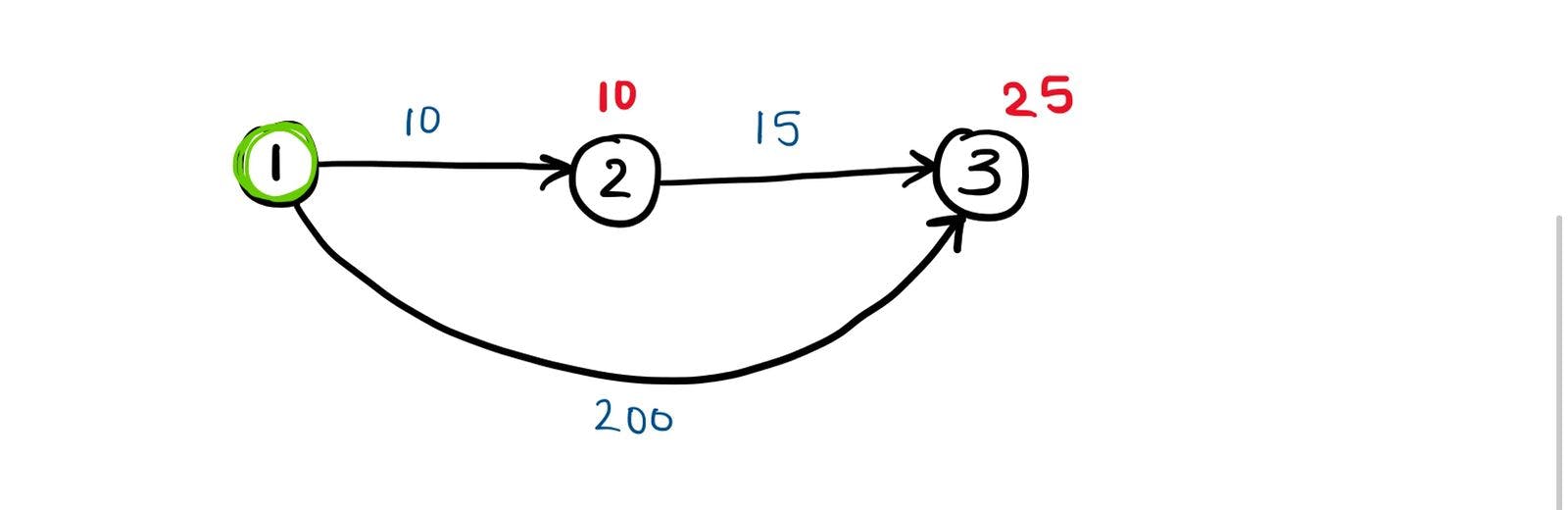
Let's apply this to the larger graph and see what happens.
Take the node connected to node 1 with the minimum distance (node 2):
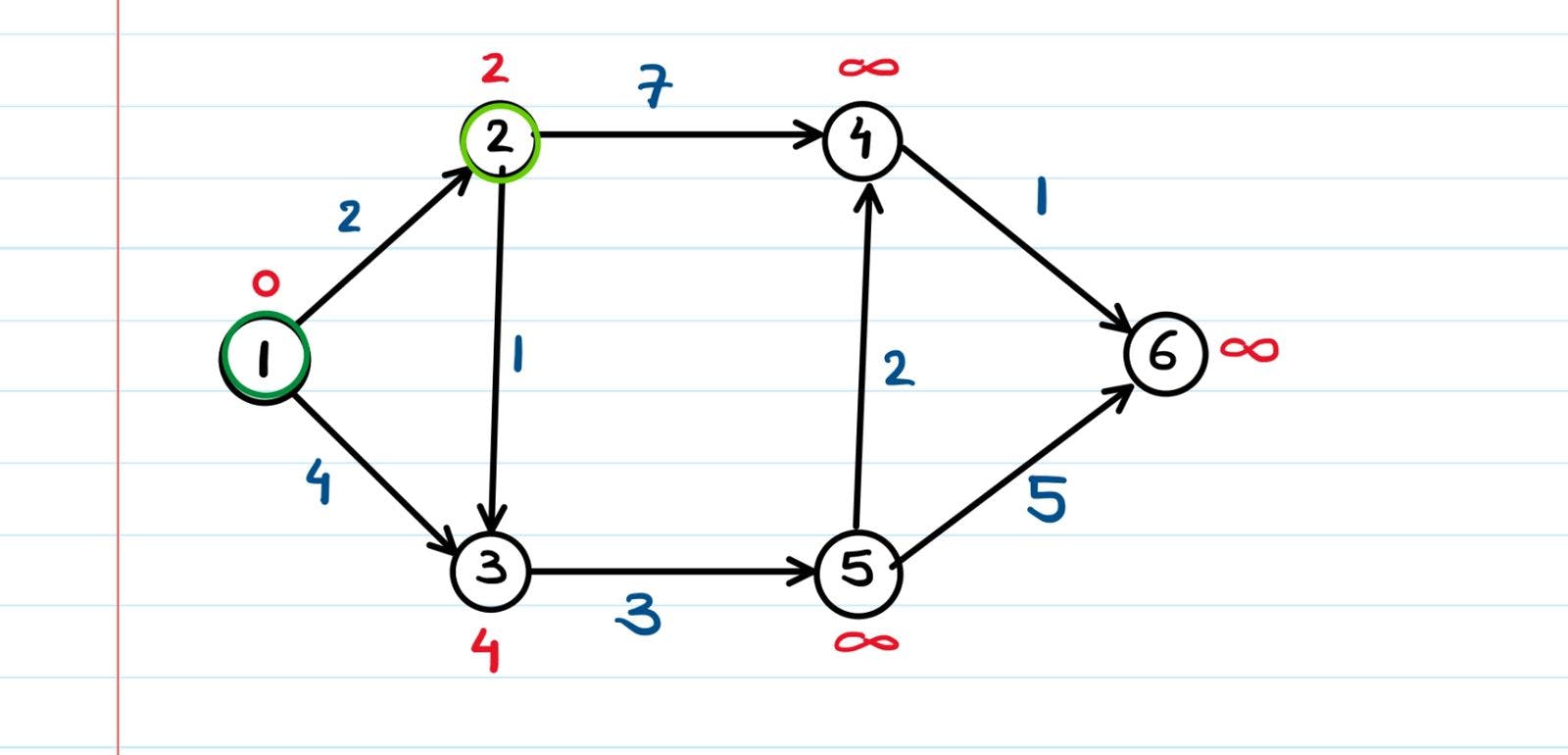
Now relax all the edges connected to node 2.
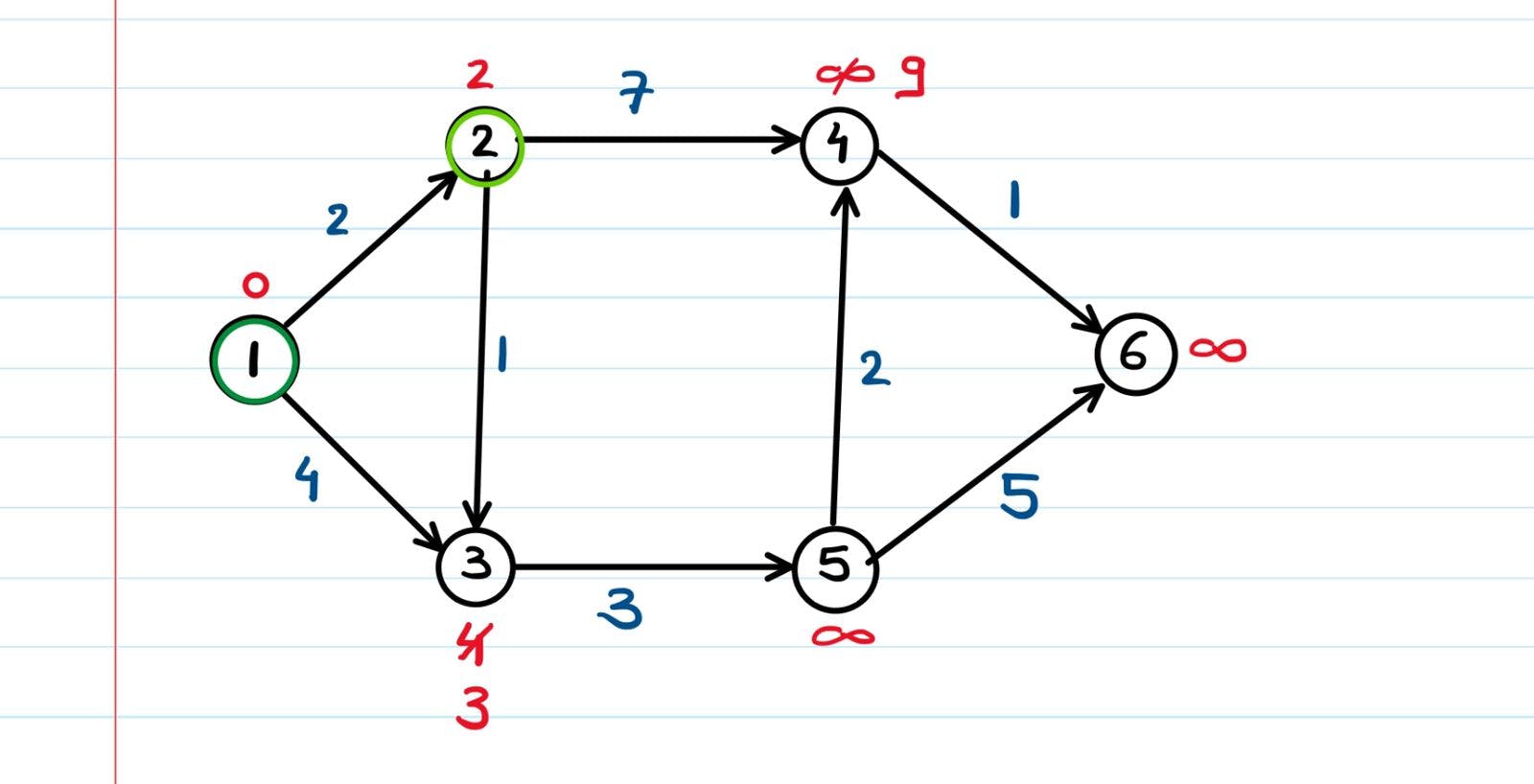
The nodes connected to node 2 were 3 and 4. If we apply the relaxation formula on them -

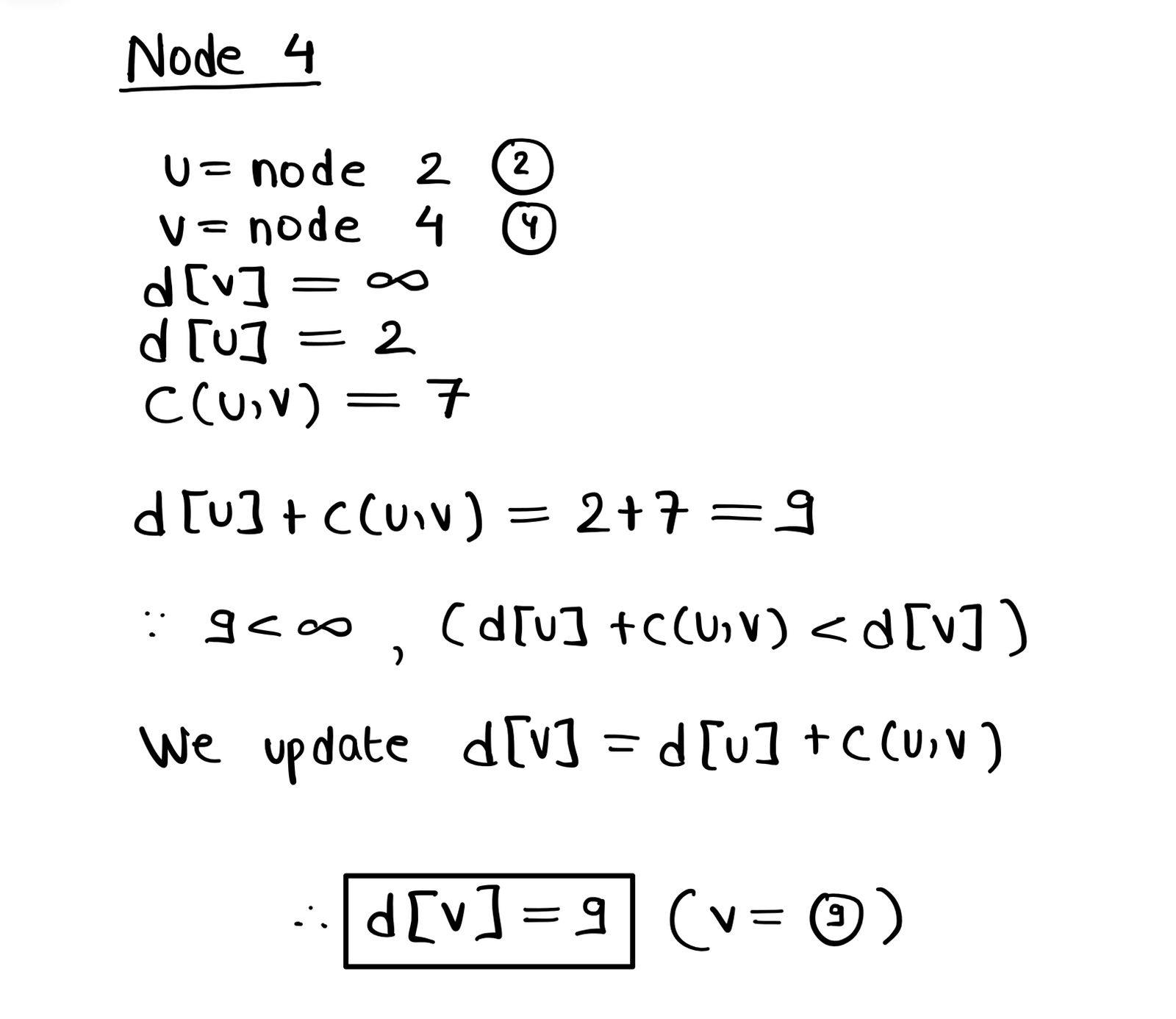
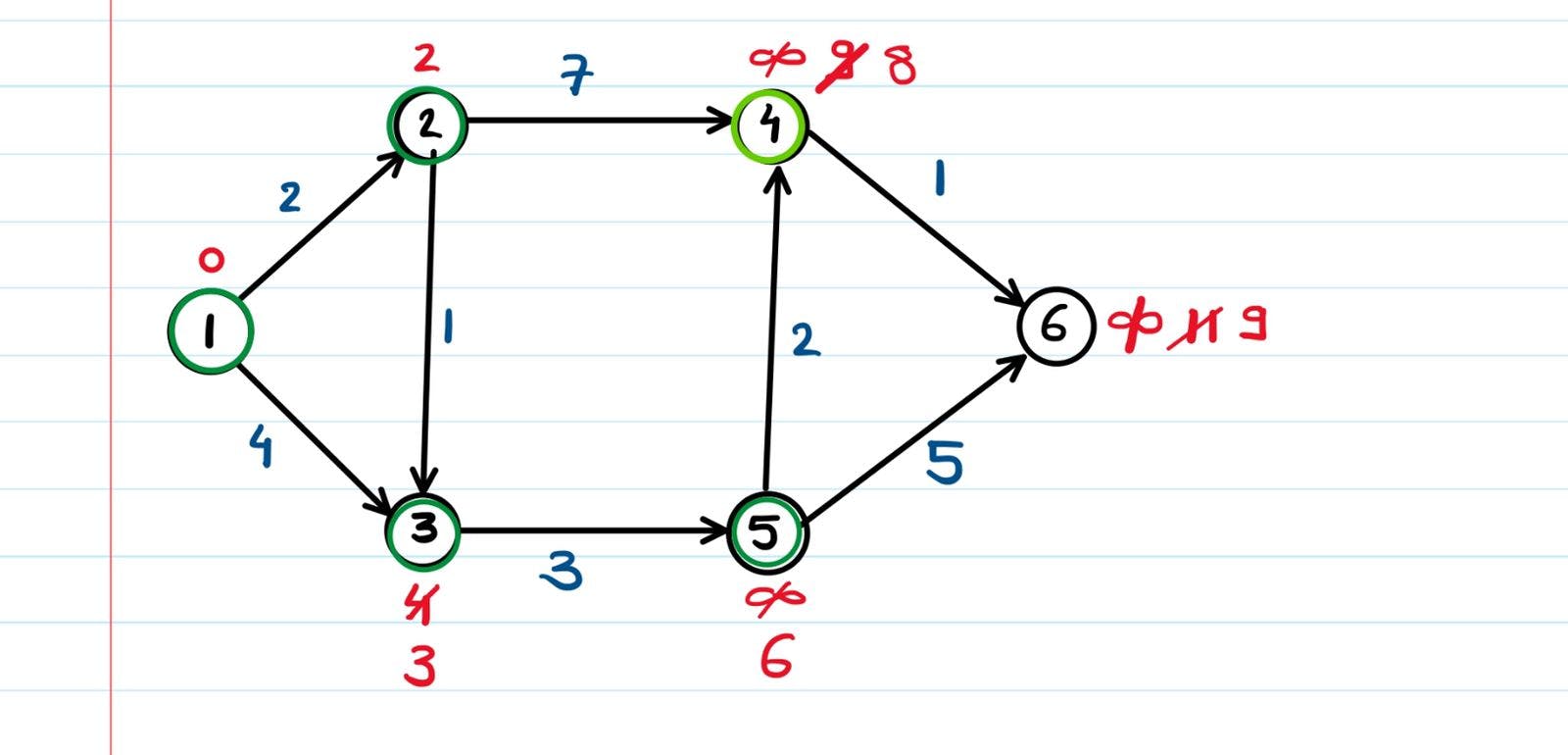
2 told its neighbors - "I can see that your at distances of 4 and infinity from the starting node. But if you take the path through me, the distance can be reduced." And hence the shortest distances were updated accordingly.
Take the minimum cost node which is connected to node 2 this time (in this case, node 3), and perform the relaxation once again.
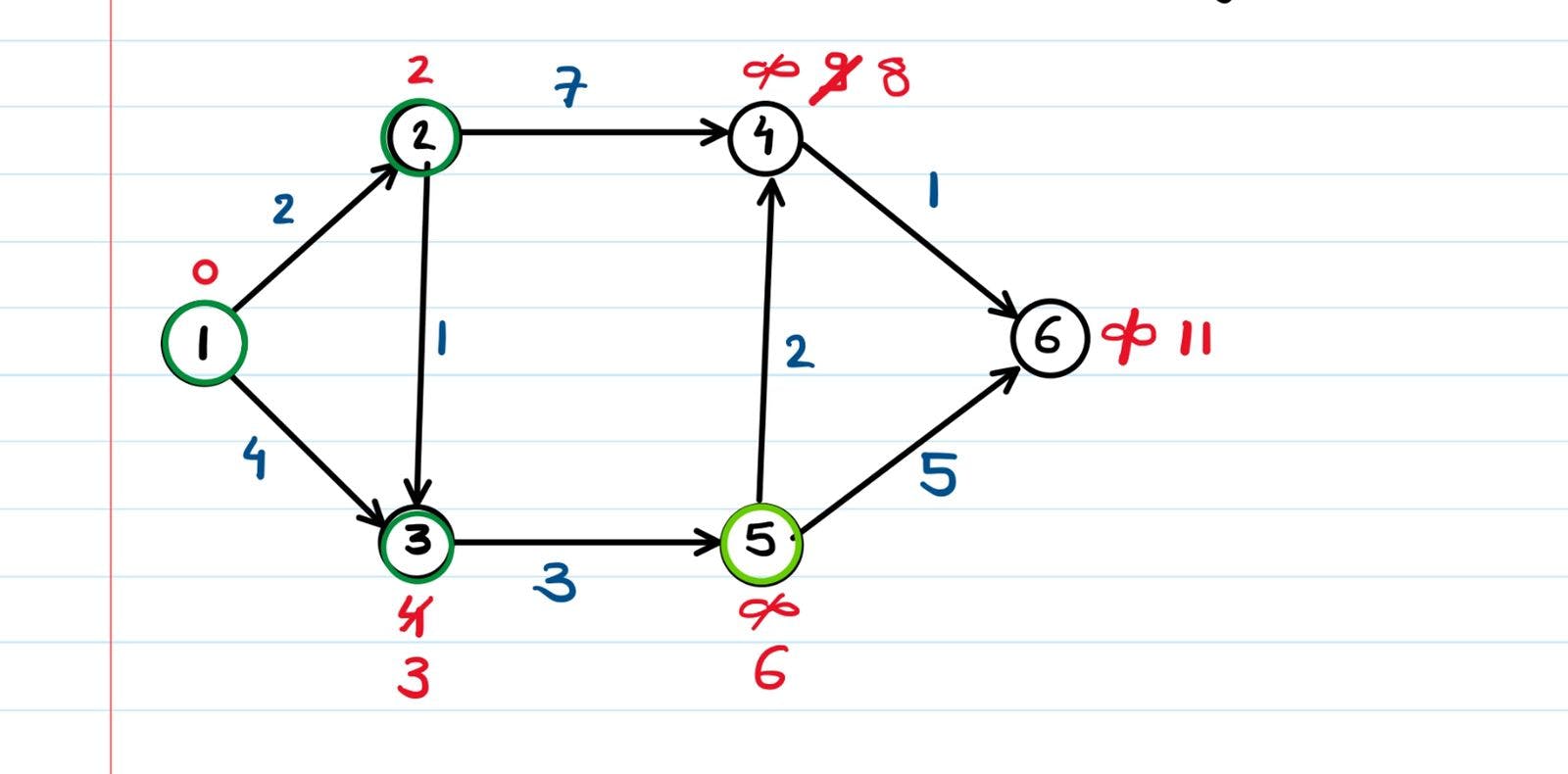
The only node which was connected to node 3 was node 5 (remember that if there's an edge from X->Y, we can only go from X to Y, but not from Y to X, hence we're not considering that node 3 can relax node 2 and node 1). Node 5's shortest distance from node 1 was updated from infinity to 6 units. We got this from the formula,

If we keep on taking the connected nodes and relaxing their adjacent edges,
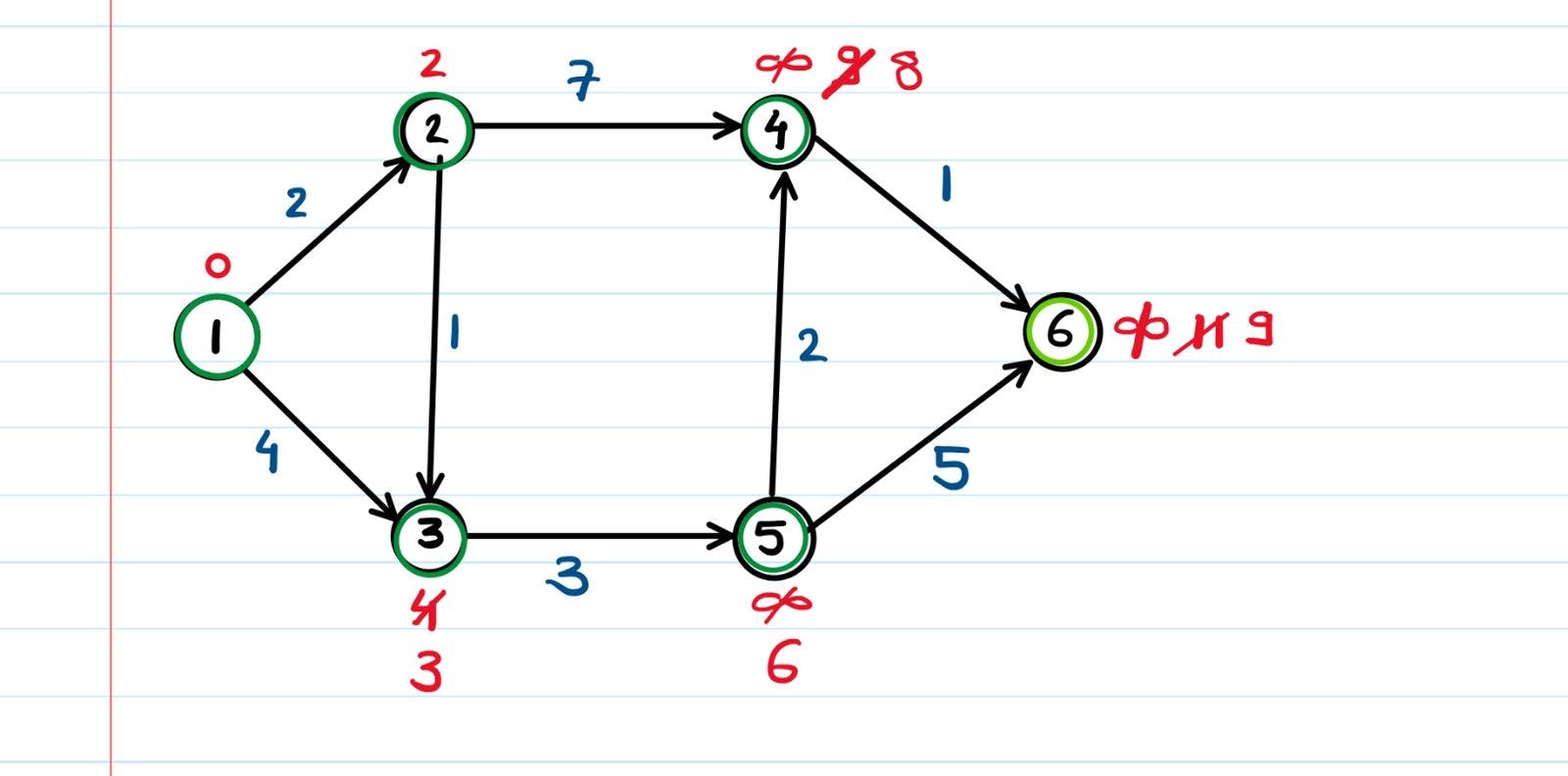
We did it ! Using the simple concept of relaxation, we now have the shortest distances of all of the nodes from the starting node.
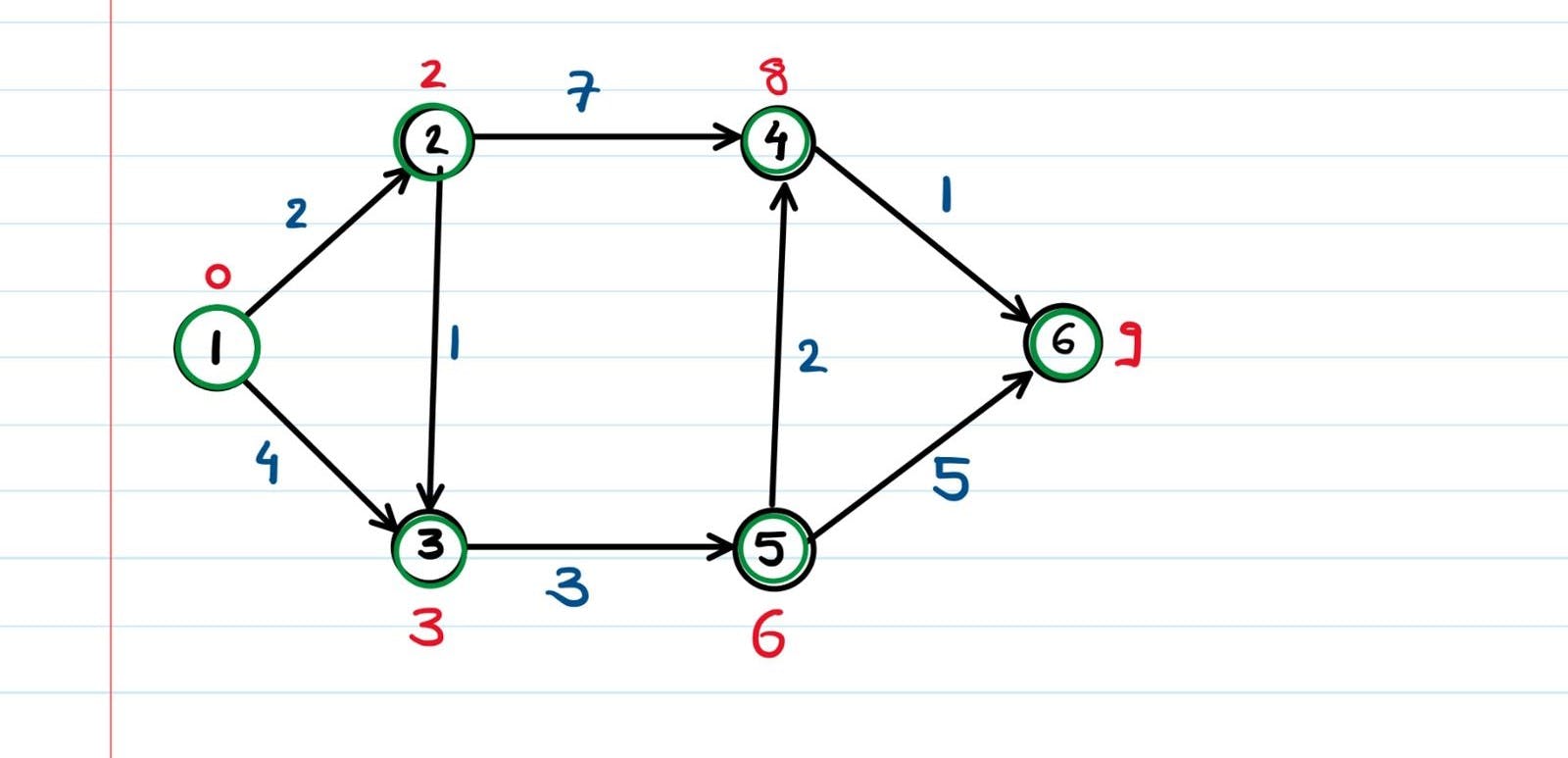
Try solving it by yourself once again so you can nail the concepts down.
The pseudocode for Dijkstra's algorithm is -
1 function Dijkstra(Graph, source):
2
3 for each vertex v in Graph.Vertices:
4 dist[v] ← INFINITY
5 prev[v] ← UNDEFINED
6 add v to Q
7 dist[source] ← 0
8
9 while Q is not empty:
10 u ← vertex in Q with min dist[u]
11 remove u from Q
12
13 for each neighbor v of u still in Q:
14 alt ← dist[u] + Graph.Edges(u, v)
15 if alt < dist[v]:
16 dist[v] ← alt
17 prev[v] ← u
18
19 return dist[], prev[]
If you want, you can code it out yourself and see the results for yourself.
Java Code-
// Dijkstra's Algorithm in Java
public class Dijkstra {
public static void dijkstra(int[][] graph, int source) {
int count = graph.length;
boolean[] visitedVertex = new boolean[count];
int[] distance = new int[count];
for (int i = 0; i < count; i++) {
visitedVertex[i] = false;
distance[i] = Integer.MAX_VALUE;
}
// Distance of self loop is zero
distance[source] = 0;
for (int i = 0; i < count; i++) {
// Update the distance between neighbouring vertex and source vertex
int u = findMinDistance(distance, visitedVertex);
visitedVertex[u] = true;
// Update all the neighbouring vertex distances
for (int v = 0; v < count; v++) {
if (!visitedVertex[v] && graph[u][v] != 0 && (distance[u] + graph[u][v] < distance[v])) {
distance[v] = distance[u] + graph[u][v];
}
}
}
for (int i = 0; i < distance.length; i++) {
System.out.println(String.format("Distance from %s to %s is %s", source, i, distance[i]));
}
}
// Finding the minimum distance
private static int findMinDistance(int[] distance, boolean[] visitedVertex) {
int minDistance = Integer.MAX_VALUE;
int minDistanceVertex = -1;
for (int i = 0; i < distance.length; i++) {
if (!visitedVertex[i] && distance[i] < minDistance) {
minDistance = distance[i];
minDistanceVertex = i;
}
}
return minDistanceVertex;
}
public static void main(String[] args) {
int graph[][] = new int[][] { { 0, 0, 1, 2, 0, 0, 0 }, { 0, 0, 2, 0, 0, 3, 0 }, { 1, 2, 0, 1, 3, 0, 0 },
{ 2, 0, 1, 0, 0, 0, 1 }, { 0, 0, 3, 0, 0, 2, 0 }, { 0, 3, 0, 0, 2, 0, 1 }, { 0, 0, 0, 1, 0, 1, 0 } };
Dijkstra T = new Dijkstra();
T.dijkstra(graph, 0);
}
}
Python Code
# Dijkstra's Algorithm in Python
import sys
# Providing the graph
vertices = [[0, 0, 1, 1, 0, 0, 0],
[0, 0, 1, 0, 0, 1, 0],
[1, 1, 0, 1, 1, 0, 0],
[1, 0, 1, 0, 0, 0, 1],
[0, 0, 1, 0, 0, 1, 0],
[0, 1, 0, 0, 1, 0, 1],
[0, 0, 0, 1, 0, 1, 0]]
edges = [[0, 0, 1, 2, 0, 0, 0],
[0, 0, 2, 0, 0, 3, 0],
[1, 2, 0, 1, 3, 0, 0],
[2, 0, 1, 0, 0, 0, 1],
[0, 0, 3, 0, 0, 2, 0],
[0, 3, 0, 0, 2, 0, 1],
[0, 0, 0, 1, 0, 1, 0]]
# Find which vertex is to be visited next
def to_be_visited():
global visited_and_distance
v = -10
for index in range(num_of_vertices):
if visited_and_distance[index][0] == 0 \
and (v < 0 or visited_and_distance[index][1] <=
visited_and_distance[v][1]):
v = index
return v
num_of_vertices = len(vertices[0])
visited_and_distance = [[0, 0]]
for i in range(num_of_vertices-1):
visited_and_distance.append([0, sys.maxsize])
for vertex in range(num_of_vertices):
# Find next vertex to be visited
to_visit = to_be_visited()
for neighbor_index in range(num_of_vertices):
# Updating new distances
if vertices[to_visit][neighbor_index] == 1 and \
visited_and_distance[neighbor_index][0] == 0:
new_distance = visited_and_distance[to_visit][1] \
+ edges[to_visit][neighbor_index]
if visited_and_distance[neighbor_index][1] > new_distance:
visited_and_distance[neighbor_index][1] = new_distance
visited_and_distance[to_visit][0] = 1
i = 0
# Printing the distance
for distance in visited_and_distance:
print("Distance of ", chr(ord('a') + i),
" from source vertex: ", distance[1])
i = i + 1
(Source - Programiz.com)
Other Fun Facts -
It has a time complexity of O(V^2) using the adjacency matrix representation of graph. The time complexity can be reduced to O((V+E)logV) using an adjacency list representation of the graph, where E is the number of edges in the graph and V is the number of vertices in the graph 📈
Dijkstra came up with the algorithm in 20 minutes while sitting at a cafe in Amsterdam with his fiance. He didn't even use a pen and paper to jot down his thinking, he worked out the magic in his mind 🧠✨.
It is used in network routing protocols such as link-state, OSPF and IS-IS 🌐
There's a cool tutorial by Clément Mihailescu where you can build your own Dijkstra pathfinding visualizer algorithm.

This blog was submitted for the 'Algorithms' track for the Hashnode and WeMakeDevs/CommunityClassroom November blogging challenge. Thanks to them for the opportunity. If you enjoyed this explanation of Dijkstra's algorithm, do check out my other articles as well. Thanks for reading ! ❤️