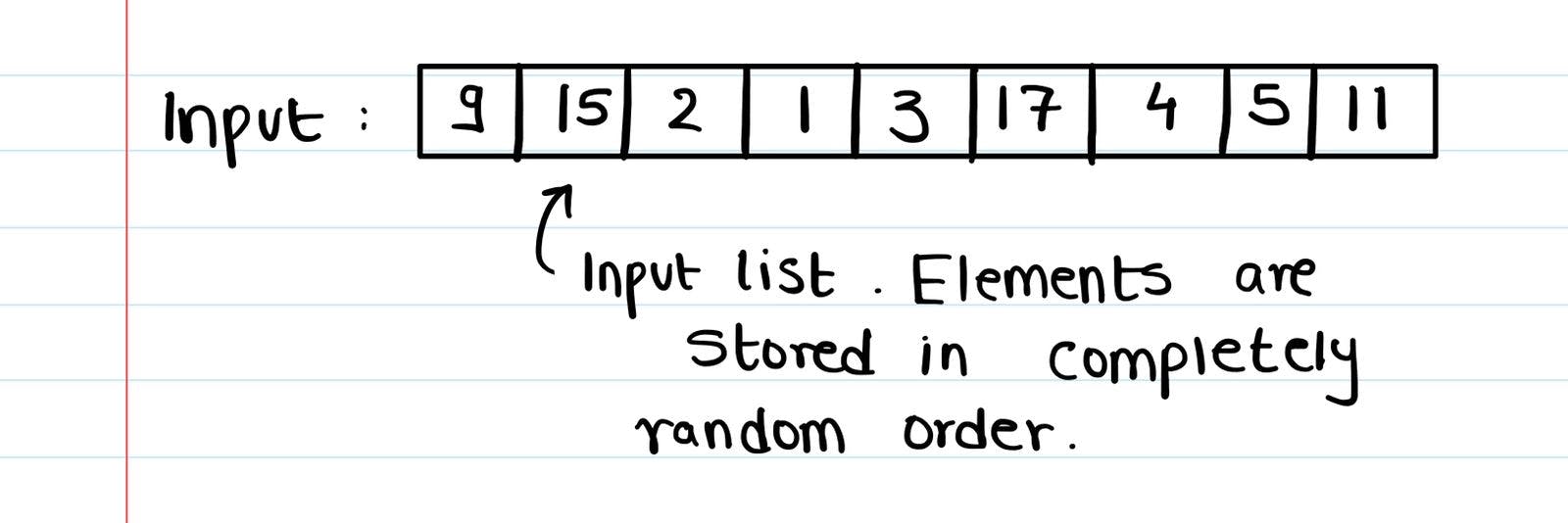
Quicksort. Merge Sort. Introsort. Heapsort. Insertion sort. Blocksort. Timsort. Bubble sort. Cocktail sort (this one sounds fun). Strandsort. Bogobogo sort. Cycle sort. There are a lot of sorting algorithms. All of them do the same thing - They take a list as an input, and arrange the elements of that list in some particular order.

You probably won't ever need to implement these algorithms from scratch. The inbuilt libraries and functions will do the heavy lifting for you. But being the passionate learner that you are, it's important to know how these algorithms work under the hood.

The sorting algorithm we'll be analyzing today is Quicksort, which uses the divide-and-conquer strategy.

How does it work ? 🔍

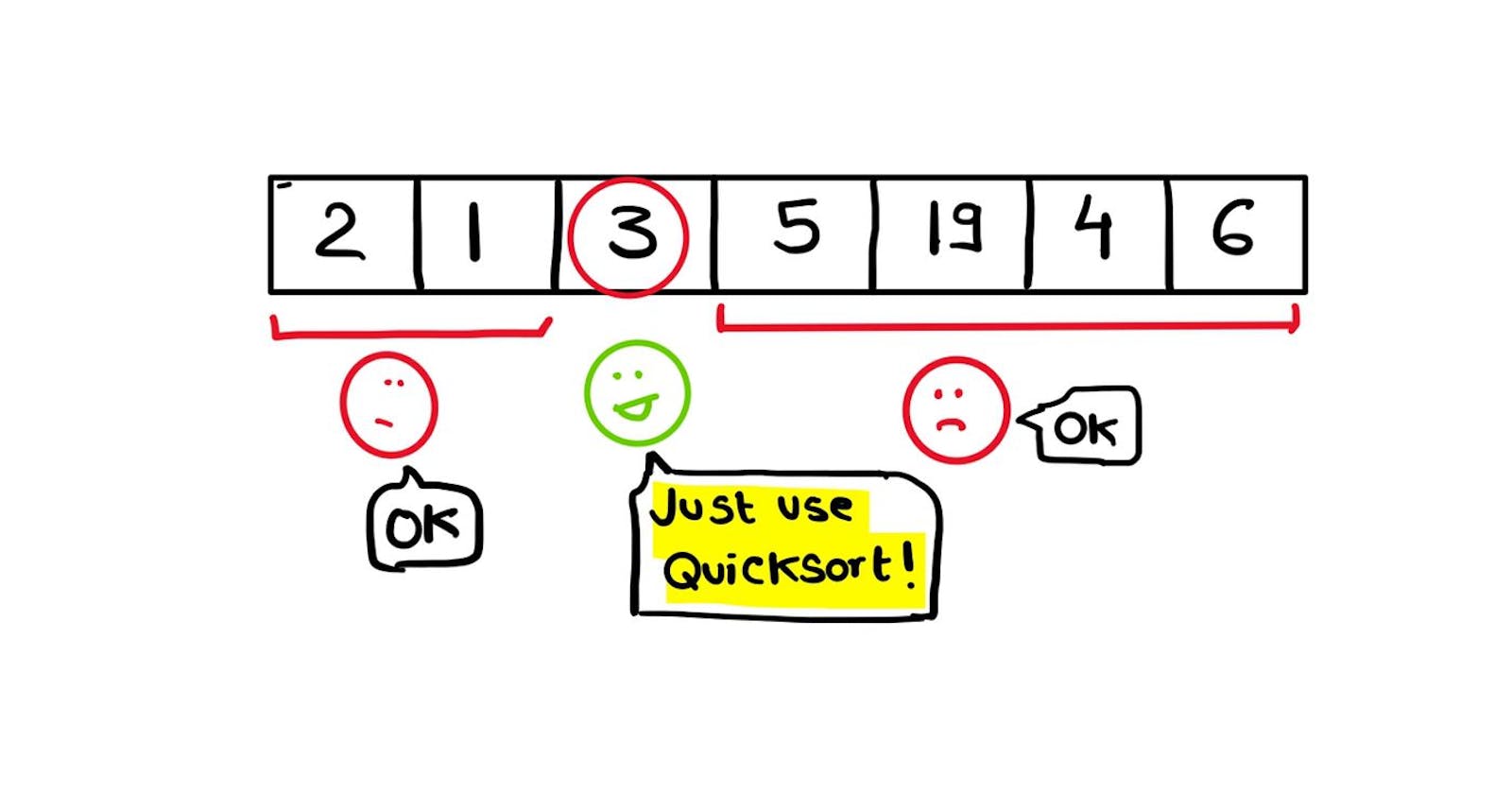
The key idea behind Quicksort is that we take an element in the array (called the pivot), place it at a position such that all the elements to its left are smaller than it, and all the elements are to its right are greater than it. The element we chose is now at it's perfect position in the final answer. We then repeat these steps again till our entire array is sorted.

This is probably difficult to understand through text, so let's look at it visually.

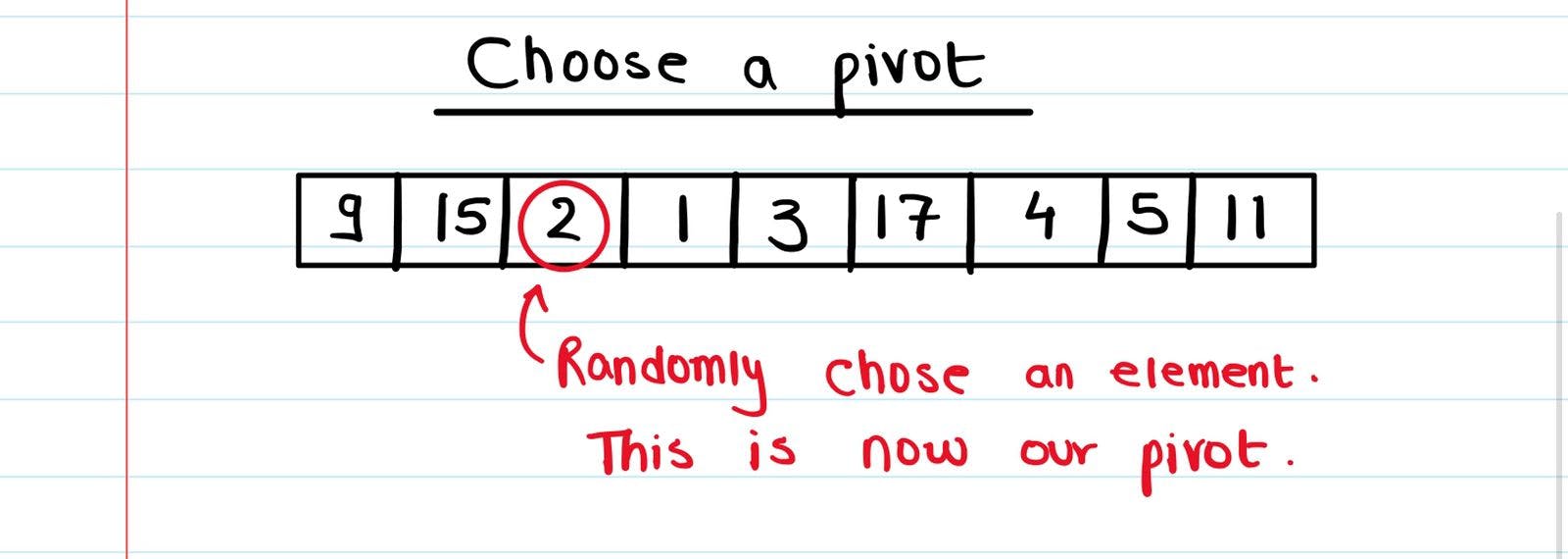
We randomly choose a pivot element (there are different methods of choosing a pivot which we'll look at later, but for now just assume we take any element on a whim).

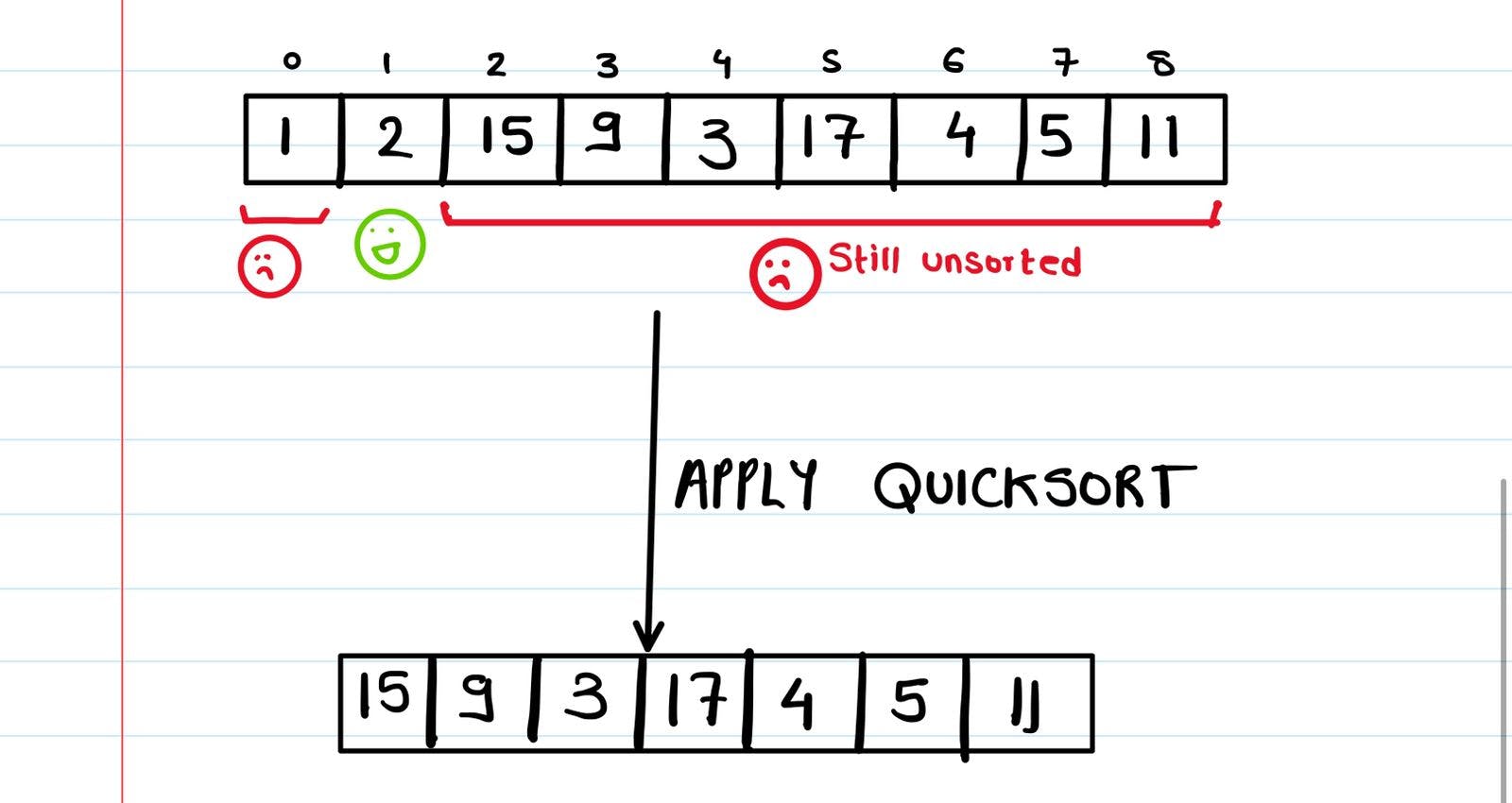
We rearrange the array so that the elements to the right of our pivot are greater than it and those to the left our pivot are smaller than it. Don't worry about how the rearrangement works for now.

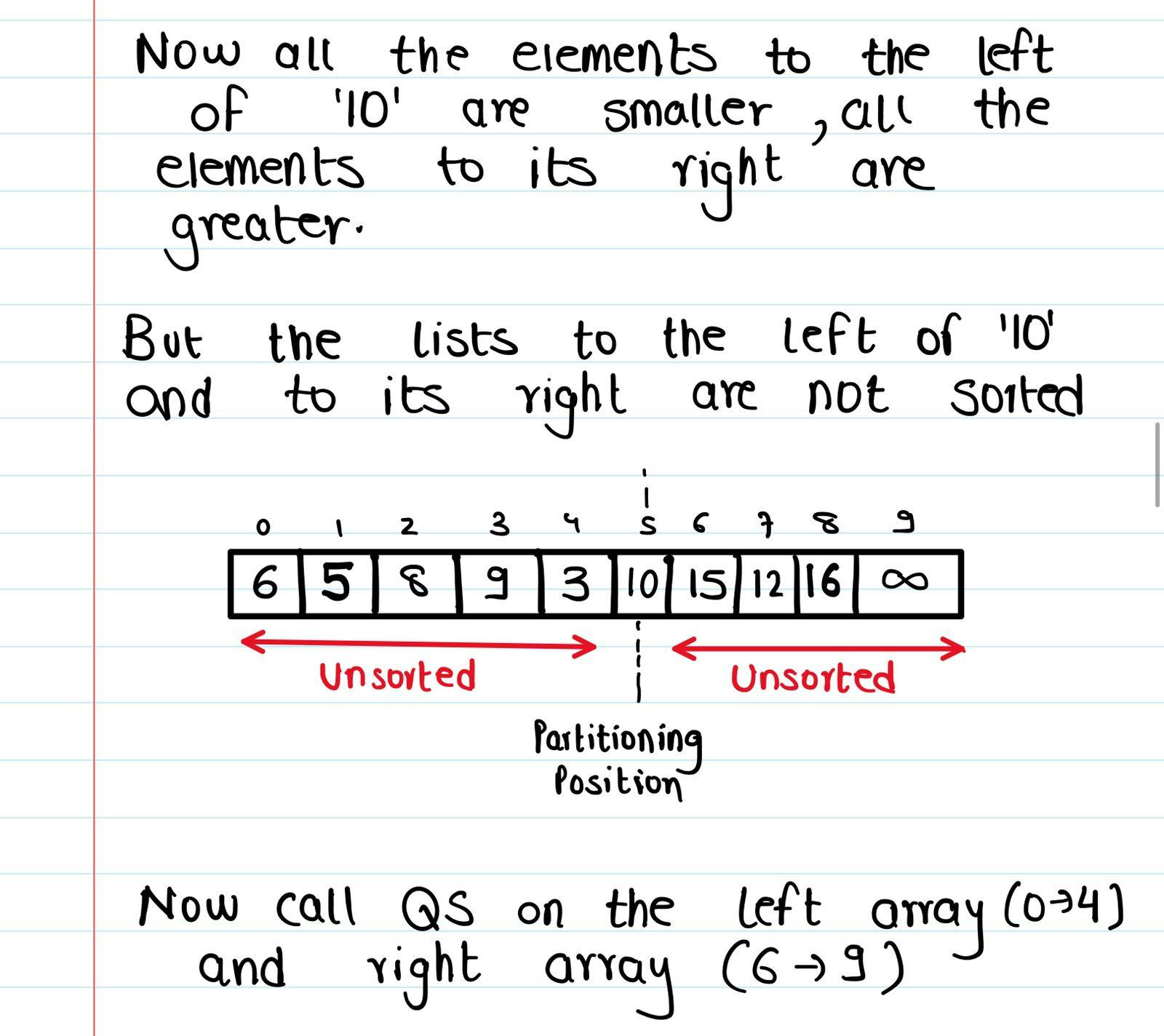
We've placed our pivot (2) at its correct index with respect to the final answer. In our final result, 2 should be at index 1, and in our current array/list, it's at index 1. Even though we've arranged the elements such that all the elements to the right of 2 are greater than it and those to the left of 2 are smaller than it, these elements are still jumbled up and not necessarily in the right position.

What now? It seems we've only managed to place 2 at the right position. What about all the elements to the left of 2? What about all the elements to the right of 2? We can't just leave them unsorted and all jumbled up. We should place them at their correct position too. But how ? If only there were a way for us the sort the list to the right of our pivot, and sort the list to the left our pivot. If only we knew about a sorting algorithm which could do that job for us.... (click here to know more about that technique).

Quicksort !

We've already seen that Quicksort can take an element (our pivot) from our unsorted array and place it at it's correct position. Now all the elements to the left and right of our pivot constitute smaller subarrays which in themselves are unsorted. To sort them, we repeat the same steps we did on our larger array, and keep on going till all our elements are sorted.

Treat the subarray to the left of the pivot as an entirely different problem. Treat the subarray to the right of the pivot as an entirely different problem. Apply Quicksort on them. Your entire array will be sorted.

Let's look at the elements to the right of our pivot (2)-

We placed 3 such that all the elements to its left are smaller than it (no such element in this case), and all the elements to its right are greater than it. Even though we've arranged the elements such that all the elements to the right of 2 are greater than it and those to the left of 3 are smaller than it, these elements are still jumbled up and not necessarily in the right position. What now? It seems we've only managed to place 3 at the right position. What about all the elements to the left of 3? What about all the elements to the right of 3? We can't just leave them unsorted and all jumbled up. We should place them at their correct position too.

Feel like you've read this explanation before ? That's because you already have ! We're just repeating the exact same steps we did for our larger array when we took 2 as the pivot. All that's changed is the elements we're taking. Once again we can use Quicksort to sort the elements to the left and right of 3.

If we consider the elements to the right of 3 - (Note that we also have to use Quicksort on the elements to the left of 3, we're just not showing it here right now)

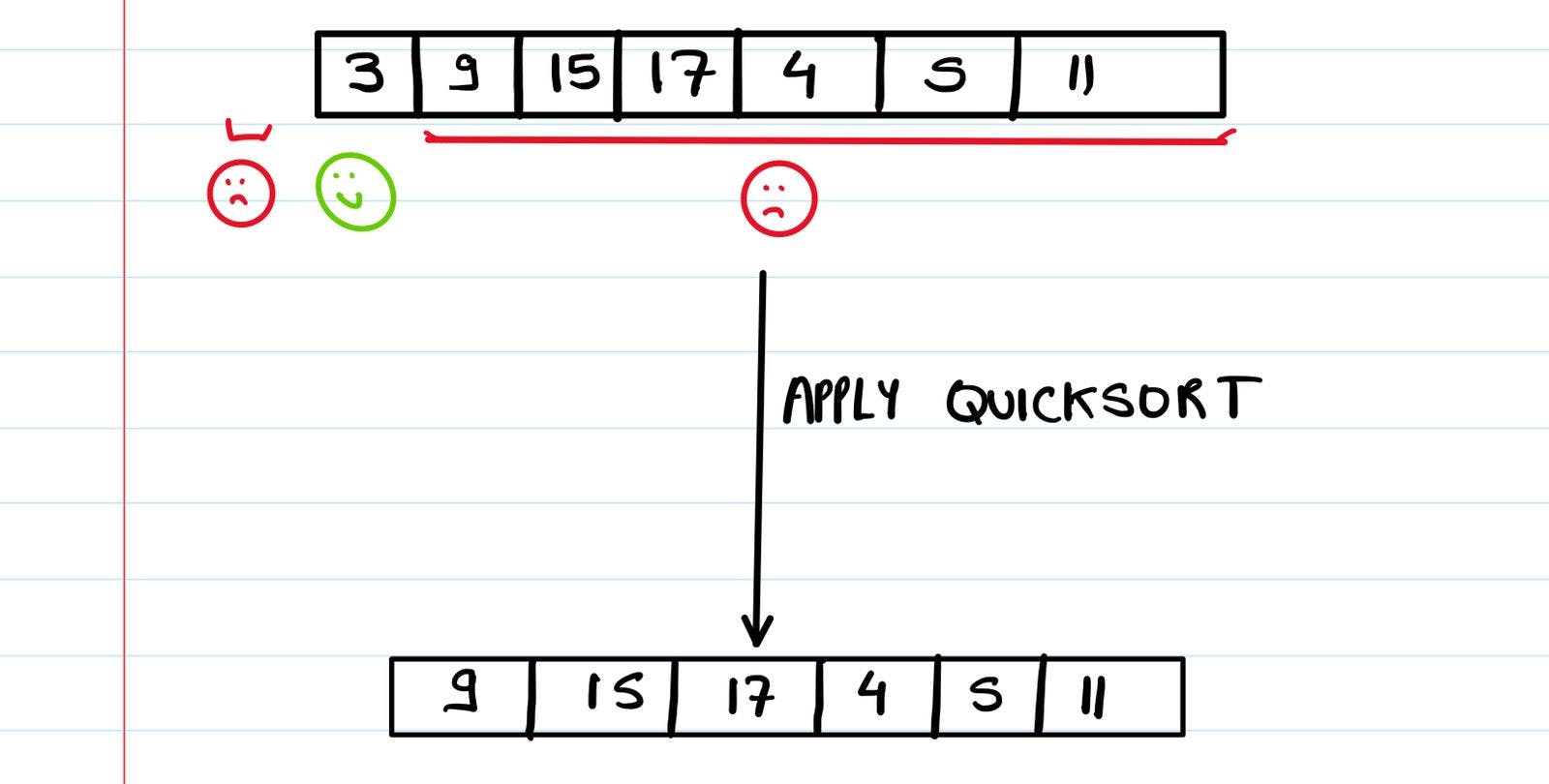
We've now placed 17 at its correct position. Again we apply Quicksort to the arrays to the left and right and right of our pivot (17) and keep on going till all our elements aren't placed at the right position.

But when should we stop ?

We've talked about using Quicksort again and again on our subarrays, but we can't keep doing this forever, right ? There has to be a point when we can tell our algorithm - "OK, there's no point in proceeding further from here. No need to use Quicksort again, our array is sorted".

Try to think about what that case could be. In what situation is our array always sorted, no matter what it contains ? (Hint - It has to do with the size of our array).

Once the subarray we're want to sort is of size 1, there's no point in calling Quicksort again, because we know that this entire array is already sorted. It only consists of 1 element, there's no possible way it CAN'T be sorted.

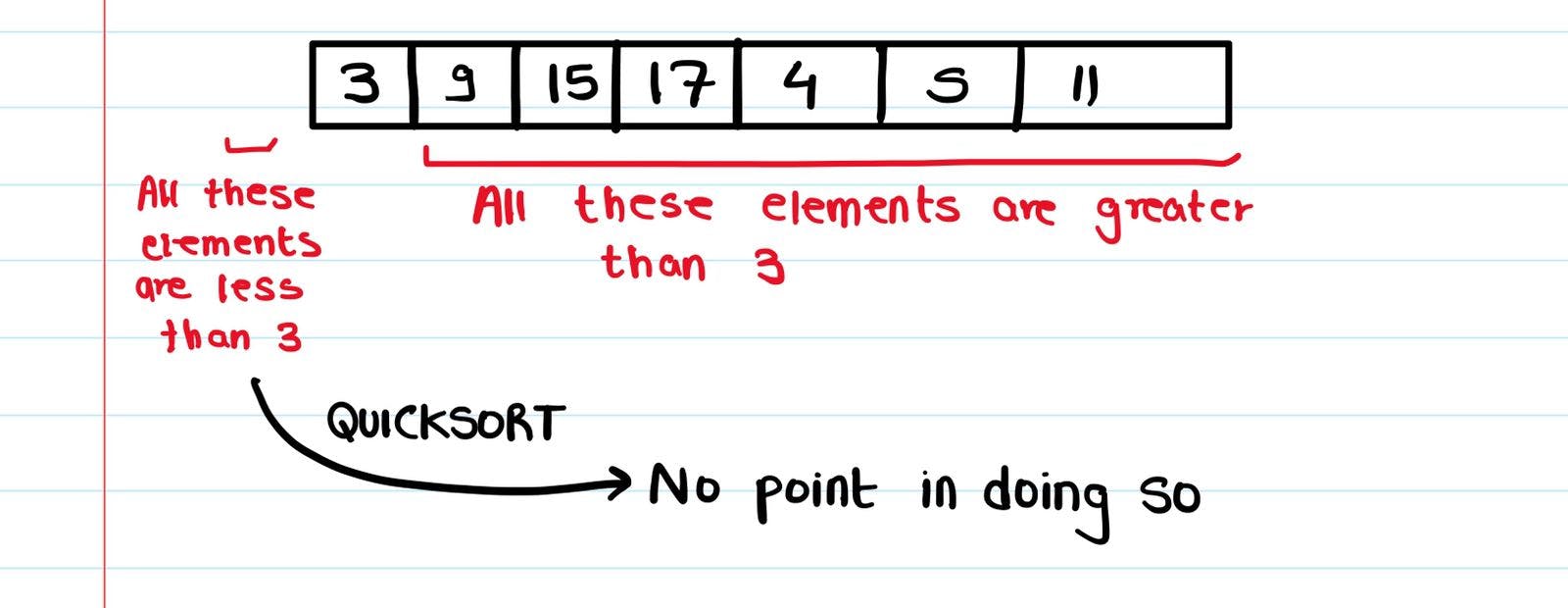
If we go back to the point when we'd taken 2 as our pivot -

The subarray/list to the left of 2 is [1]. If we use Quicksort to sort this array,

Similarly, if we look at the point when 3 was the pivot, the list/subarray to the left of 3 was empty and contained no elements. There's no point in sorting a list which contains no elements, since that doesn't mean anything.

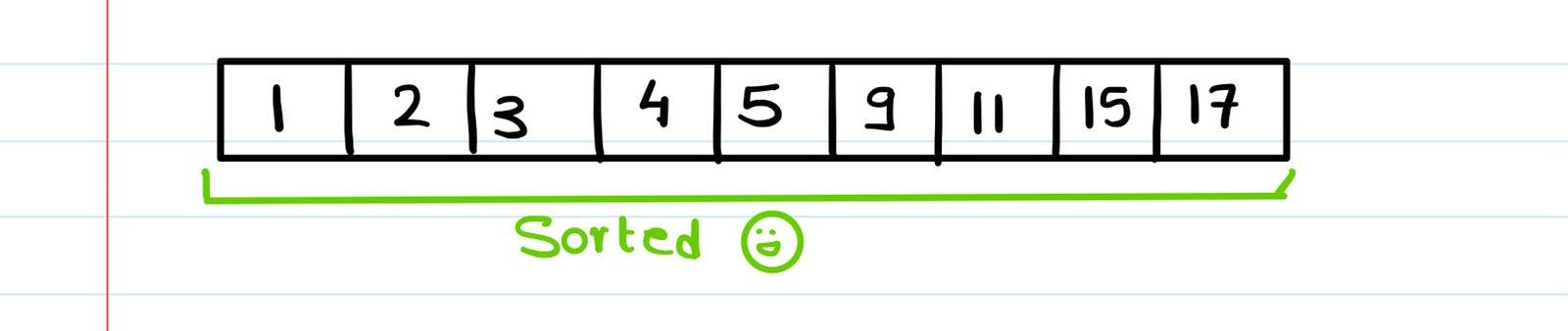
So we stop using Quicksort when either the array is of size 1 or 0.

We keep on solving until our entire array is sorted. You can use this visualizer to check out all the steps involved.

We still haven't discussed 2 things yet :

• How we place the pivot and rearrange the array such that the elements to its left are smaller than it, and the elements to its right are greater than it
• How we choose the pivot

Rearranging the array and the pivot

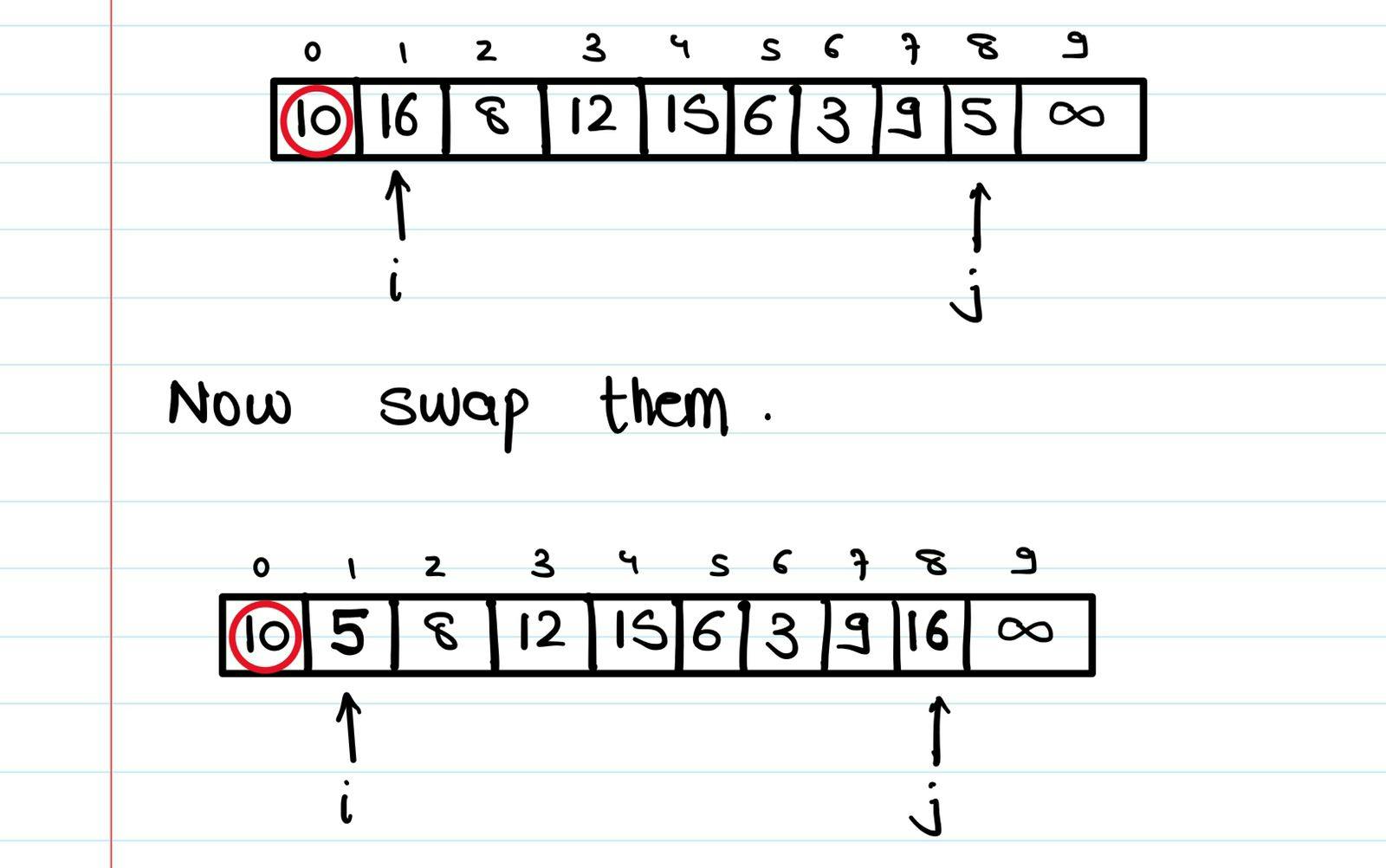
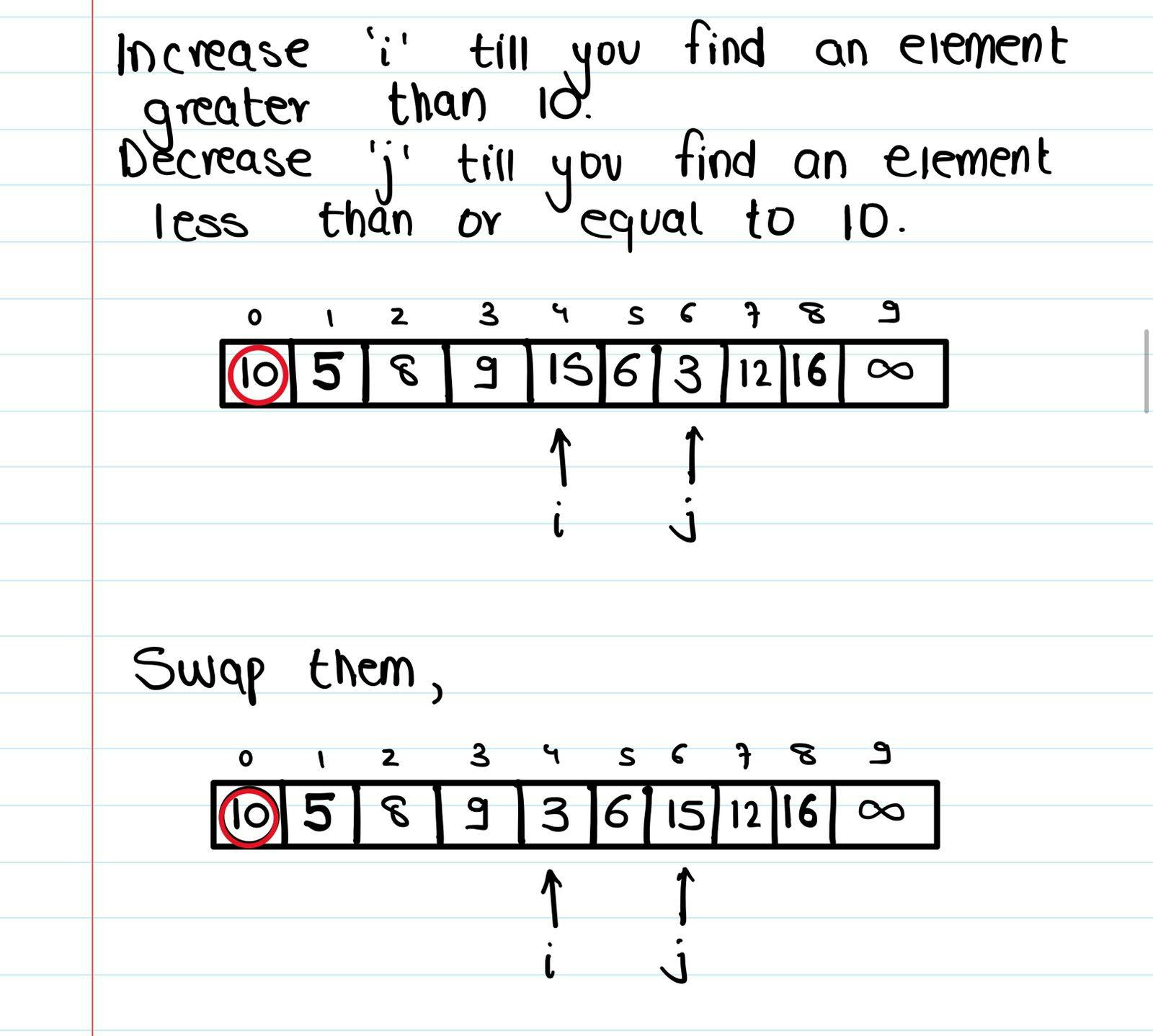
⬆️ We use 2 pointers to help us place the pivot at it's correct position. One pointer moves from left to right, and searches for elements which are greater than the pivot. The other pointer moves from right to left, and searches for elements which are smaller than the pivot. What both these pointers are basically doing is finding violations. They're searching for elements which are disobeying the property - elements smaller than the pivot to its left, greater elements to its right. Once both these pointers have found violations, they swap their elements so that the violations are eliminated. The element which is greater goes to the right, and the element which is smaller goes to the left.

If we take an example where we take the first element as the pivot -

Selecting the pivot

Does it really matter which element we choose as the pivot ? After all, after the rearrangement it'll find itself at the correct position and we can sort the remaining parts of the array. For most cases, no, it doesn't really matter.

But we have to see how the pivot affects the time complexity of our algorithm. Remember how the pivot splits our array into 2 parts on which we have to apply Quicksort again ? Well depending on where the pivot ends up can drastically affect the time complexity of our program.

Suppose the length of our array is 'n'. Suppose after the rearrangement our pivot ends up at index 'k' (k<n). Now there are 'k' elements to the left of our pivot and 'n-k-1' elements to the right of our pivot.

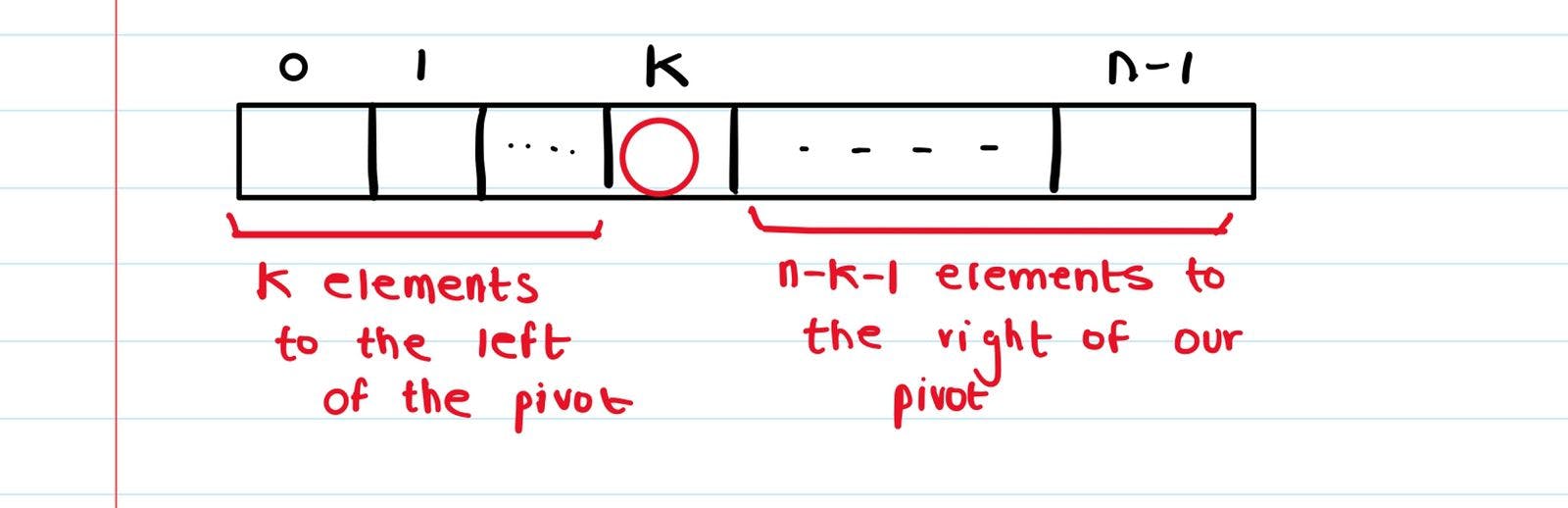
So the time complexity of our algorithm will be - T(k) + T(n-k-1) + O(n)

At each step our algorithm divides our problem into 2 sub-problems of different sizes. The size of these problems depends on where our pivot ends up.

If the pivot always ends up at the beginning or ending of the list, then at each step our 2 sub-problems are of size 0 and 'n-1', where 'n' is the size of the array. Therefore at each step we again need to solve a problem of a nearly similar size to the problem we had before ('n' and 'n-1'). This leads to worst time complexity of O(n^2).

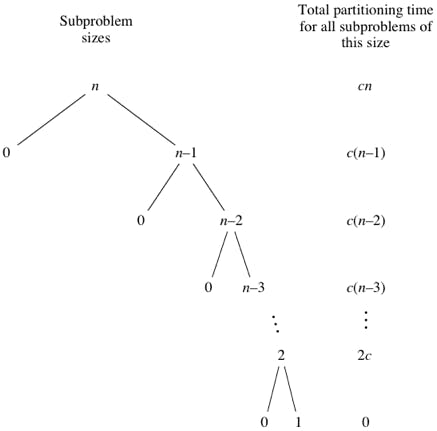
If we're taking the first/last element as the pivot and rearranging the list, it won't always be a problem, since the pivot may find itself somewhere in the middle after the rearrangement.

The issue arises when we're taking the first/last element as the pivot AND the list is already sorted. In that case, even after the rearrangement our pivot is still at the first/last position and our sub-problem is of size 'n-1' and we get a time complexity of O(n^2).

The ideal case is when our pivot ends up right in the middle of the array and divides the problem into 2 sub-problems of equal/almost equal sizes. In that case the time complexity of Quicksort becomes O(nlog(n)).

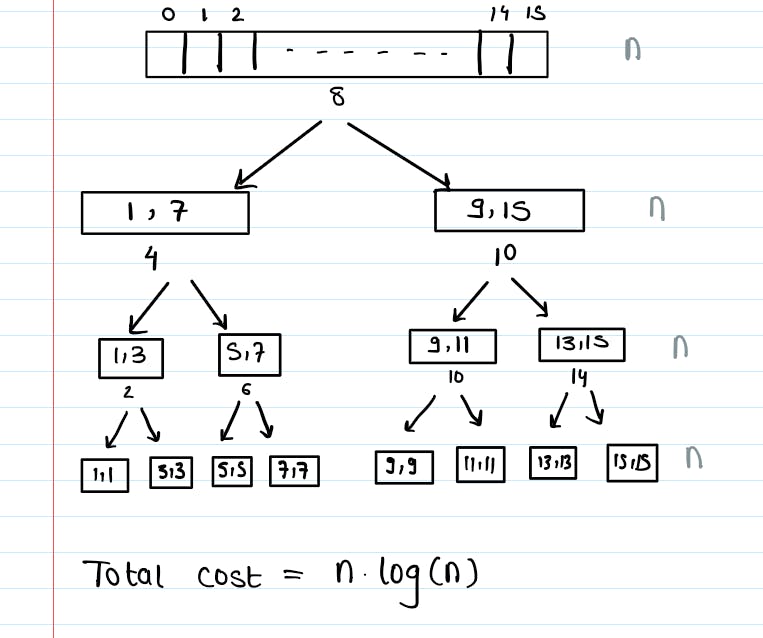
However this cannot always be guaranteed to happen and we need to be lucky enough that the pivot we chose was the median of all the elements in the array, so that after the rearrangement it lands in the middle and we get what we want. But we can use this to solve the problem we had when our list was already sorted and we were taking the first/last element as the pivot. If our list is already sorted, we can take the middle element as the pivot, so that each time our problem is divided into 2 equal subproblems and the time complexity becomes O(nlog(n)).

So in short, it doesn't really matter which element you choose as the pivot since we can't say where the pivot will end up after the rearrangement. But in the worst case that the array is already sorted, we don't want to take the first/last element as the pivot since it'll give a time complexity of O(n^2). Taking the pivot as the middle element is a safer bet in that case. A few implementations of Quicksort randomly choose the pivot. Some implementations use the 'median of 3' selection rule. You can read more about the topic here.

Time Complexities :

• Worst Case Complexity O(n^2) It occurs when the pivot element picked is either the greatest or the smallest element. This condition leads to the case in which the pivot element lies in an extreme end of the sorted array. One sub-array is always empty and another sub-array contains n - 1 elements. Thus, Quicksort is called only on this sub-array.
• Best Case Complexity O(nlogn) It occurs when the pivot element is always the middle element
• Average Case Complexity O(nlogn) It occurs when the above conditions do not occur.

Pseudocode and Code

Pseudocode:

// Sorts a (portion of an) array, divides it into partitions, then sorts those
algorithm quicksort(A, lo, hi) is 
  if lo >= 0 && hi >= 0 && lo < hi then
    p := partition(A, lo, hi) 
    quicksort(A, lo, p) // Note: the pivot is now included
    quicksort(A, p + 1, hi) 

// Divides array into two partitions
algorithm partition(A, lo, hi) is 
  // Pivot value
  pivot := A[ floor((hi + lo) / 2) ] // The value in the middle of the array

  // Left index
  i := lo - 1 

  // Right index
  j := hi + 1

  loop forever 
    // Move the left index to the right at least once and while the element at
    // the left index is less than the pivot
    do i := i + 1 while A[i] < pivot

    // Move the right index to the left at least once and while the element at
    // the right index is greater than the pivot
    do j := j - 1 while A[j] > pivot

    // If the indices crossed, return
    if i >= j then return j

    // Swap the elements at the left and right indices
    swap A[i] with A[j]

Code :

public int[] sortArray(int[] nums) {
        quickSortWithRecursion(0, nums.length - 1, nums);

        return nums;
    }

    public void quickSortWithRecursion(int low, int high, int[] work) {
        if (low >= high) return;

        int left = low, right = high;
        int pivot = work[(low + high) / 2];

        while (left <= right) {
            while (work[left] < pivot) left++;
            while (work[right] > pivot) right--;
            if (left > right) break;

            swap(left, right, work);
            left++;
            right--;
        }

        quickSortWithRecursion(low, right, work);
        quickSortWithRecursion(left, high, work);
    }

    public void swap(int i, int j, int[] array) {
        int temp = array[i];
        array[i] = array[j];
        array[j] = temp;
    }

Other Fun Facts

• Quicksort is an unstable sorting algorithm

• It was discovered by Turing Award recipient, Tony Hoare in 1959 🧠

• It is used in is Java's internal sorting algorithms along with Timsort ♨️

This blog was submitted for the 'Algorithms' track for the Hashnode and WeMakeDevs/CommunityClassroom November blogging challenge. Thanks to them for the opportunity. If you enjoyed this explanation of the Quicksort algorithm, do check out my other articles as well. Thanks for reading ! ❤️